[Fluent python] Chapter 1. The python data model

Khám phá thế giới cấu trúc dữ liệu Python! Note này sẽ hướng dẫn bạn về List, Tuple, Dictionary, Set và các khái niệm quan trọng như khả năng thay đổi, tham chiếu đối tượng. Cùng nhau nâng cao kỹ năng lập trình Python thông qua việc tổ chức và lưu trữ dữ liệu hiệu quả!

Table of content

A Pythonic Card Deck
How Special Methods Are Used
- 2.1. Emulating Numeric Types
- 2.2. String Representation
- 2.3. Boolean Value of a Custom Type
- 2.4. Collection API
Overview of Special Methods
Why len Is Not a Method

Example notebook

1. A Pythonic Card Deck

import collections

Card = collections.namedtuple('Card', ['rank', 'suit'])

class FrenchDeck:
    ranks = [str(n) for n in range(2, 11)] + list('JQKA')
    suits = 'Zô Cơ Bích Tép'.split()

    def __init__(self):
        self._cards = [Card(rank, suit) for rank in self.ranks for suit in self.suits]
    
    def __len__(self):
        return len(self._cards)
    
    def __getitem__(self, position):
        return self._cards[position]

Điều đầu tiên cần lưu ý là việc sử dụng collections.namedtuple để xây dựng một lớp đơn giản đại diện cho từng quân bài. Chúng ta sử dụng namedtuple để tạo ra các lớp đối tượng chỉ là tập hợp các thuộc tính mà không có phương thức tùy chỉnh nào, giống như một bản ghi cơ sở dữ liệu.

Trong ví dụ này, chúng ta sử dụng nó để cung cấp một cách biểu diễn đẹp mắt cho các quân bài trong bộ bài, như được hiển thị trong phiên làm việc trên console:

>>> beer_card = Card('7', 'diamonds')
>>> beer_card
Card(rank='7', suit='diamonds')

Công cụ này giúp tạo ra các kiểu dữ liệu đơn giản, giống như một cách để lưu trữ thông tin. Trong trường hợp này, nó được dùng để tạo ra một kiểu dữ liệu “quân bài” với hai thuộc tính là “rank” (hạng) và “suit” (chất).

Tuy nhiên, điểm mấu chốt của ví dụ này nằm ở lớp FrenchDeck. Mặc dù ngắn gọn, nhưng nó chứa đựng nhiều sức mạnh.

Đầu tiên, giống như bất kỳ tập hợp Python tiêu chuẩn nào, một bộ bài (deck) phản hồi hàm len() bằng cách trả về số lượng quân bài trong đó:

>>> deck = FrenchDeck()
>>> len(deck)
52

Việc đọc các quân bài cụ thể từ bộ bài - chẳng hạn như quân bài đầu tiên hoặc cuối cùng - rất dễ dàng, nhờ phương thức __getitem__:

>>> deck[0]
Card(rank='2', suit='spades')
>>> deck[-1]
Card(rank='A', suit='hearts')

Chúng ta có nên tạo một phương thức để chọn một quân bài ngẫu nhiên không? Không cần thiết. Python đã có sẵn một hàm để lấy một phần tử ngẫu nhiên từ một chuỗi: random.choice. Chúng ta có thể sử dụng nó trên một instance của bộ bài:

>>> from random import choice
>>> choice(deck)
Card(rank='3', suit='hearts')
>>> choice(deck)
Card(rank='K', suit='spades')
>>> choice(deck)
Card(rank='2', suit='clubs')

Chúng ta vừa thấy hai lợi ích của việc sử dụng các phương thức đặc biệt để tận dụng python data model:

Người dùng không phải ghi nhớ các tên phương thức tùy ý cho các thao tác tiêu chuẩn. (“Làm thế nào để lấy số lượng phần tử? Là .size(), .length(), hay cái gì khác?”)
Dễ dàng hơn để hưởng lợi từ Python standard library và tránh việc “phát minh lại bánh xe”, như hàm random.choice.

But it gets better.

Vì __getitem__ delegates cho toán tử [] của self._cards, bộ bài của chúng ta tự động hỗ trợ slicing:

>>> deck[:3]
[Card(rank='2', suit='spades'), Card(rank='3', suit='spades'), Card(rank='4', suit='spades')]
>>> deck[12::13] #deck[start:stop:step]
[Card(rank='A', suit='spades'), Card(rank='A', suit='diamonds'), Card(rank='A', 'suit='clubs'), Card(rank='A', suit='hearts')]

Chỉ bằng cách triển khai phương thức đặc biệt __getitem__, chúng ta cũng có thể chạy các vòng lặp:

>>> for card in deck: # doctest: +ELLIPSIS
...     print(card)
Card(rank='2', suit='spades')
Card(rank='3', suit='spades')
Card(rank='4', suit='spades')
...

Theo thứ tự ngược lại:

>>> for card in reversed(deck):
...     print(card)
Card(rank='A', suit='hearts')
Card(rank='K', suit='hearts')
Card(rank='Q', suit='hearts')
...

Việc lặp lại thường là ngầm định. Nếu một tập hợp không có phương thức __contains__, toán tử in sẽ thực hiện quét tuần tự. Trường hợp điển hình: in hoạt động với lớp FrenchDeck của chúng ta vì nó có thể lặp lại được. Hãy xem thử:

>>> Card('Q', 'hearts') in deck
True
>>> Card('7', 'beasts') in deck
False

Còn việc sắp xếp thì sao? Một hệ thống xếp hạng quân bài phổ biến là theo hạng (với quân Át là cao nhất), sau đó theo chất theo thứ tự bích (cao nhất), cơ, rô và chuồn (thấp nhất). Dưới đây là một hàm xếp hạng quân bài theo quy tắc đó, trả về 0 cho quân 2 chuồn và 51 cho quân Át bích:

suit_values = dict(spades=3, hearts=2, diamonds=1, clubs=0)

def spades_high(card):
    rank_value = FrenchDeck.ranks.index(card.rank)
    return rank_value * len(suit_values) + suit_values[card.suit]

Với hàm spades_high, giờ đây chúng ta có thể liệt kê bộ bài theo thứ tự tăng dần:

>>> for card in sorted(deck, key=spades_high):
...     print(card)
Card(rank='2', suit='clubs')
Card(rank='2', suit='diamonds')
Card(rank='2', suit='hearts')
... (46 cards omitted)
Card(rank='A', suit='diamonds')
Card(rank='A', suit='hearts')
Card(rank='A', suit='spades')
# doctest: +ELLIPSIS

Mặc dù FrenchDeck kế thừa ngầm định từ lớp object, nhưng hầu hết chức năng của nó không phải được kế thừa mà đến từ việc tận dụng data model và kỹ thuật composition. Bằng cách triển khai các phương thức đặc biệt __len__ và __getitem__, lớp FrenchDeck của chúng ta hoạt động giống như một standard Python sequence, cho phép nó hưởng lợi từ các tính năng cốt lõi của ngôn ngữ (ví dụ: iteration và slicing)) và từ standard library, như được hiển thị trong các ví dụ sử dụng random.choice, reversed và sorted. Nhờ kỹ thuật composition, việc triển khai __len__ và __getitem__ có thể delegate toàn bộ công việc cho một đối tượng list, self._cards.

2. How Special Methods Are Used

Phương thức đặc biệt (special methods), còn được gọi là phương thức ma thuật (magic methods) hoặc phương thức dunder, là những phương thức có tên được định nghĩa trước trong Python, bắt đầu và kết thúc bằng hai dấu gạch dưới (ví dụ: __init__, __len__, __str__).
Chúng ta thường tương tác với các phương thức đặc biệt một cách gián tiếp thông qua các hàm tích hợp sẵn hoặc các toán tử. Ví dụ, khi bạn sử dụng toán tử + để cộng hai số, Python sẽ gọi phương thức __add__ của lớp số tương ứng.
Việc sử dụng phương thức đặc biệt cho phép chúng ta định nghĩa cách các đối tượng của lớp do người dùng định nghĩa tương tác với các hàm và toán tử tích hợp sẵn, giúp mã trở nên rõ ràng và dễ đọc hơn.
Một số ví dụ về cách sử dụng phương thức đặc biệt bao gồm:
- Định nghĩa cách một đối tượng được biểu diễn dưới dạng chuỗi bằng cách triển khai phương thức __str__.
- Xác định hành vi của một đối tượng khi được sử dụng với toán tử so sánh bằng cách triển khai các phương thức như __lt__ (nhỏ hơn), __gt__ (lớn hơn), __eq__ (bằng).
- Tạo các lớp giống như collection bằng cách triển khai các phương thức như __len__, __getitem__, __setitem__.
Trình thông dịch Python tối ưu hóa việc gọi các phương thức đặc biệt đối với các kiểu dữ liệu tích hợp sẵn, giúp tăng hiệu suất.

Tóm lại, phương thức đặc biệt là một phần quan trọng của Python, cho phép chúng ta tạo ra các lớp linh hoạt và mạnh mẽ, tương tác liền mạch với ngôn ngữ.

2.1. Emulating Numeric Types

Một số phương thức đặc biệt cho phép các đối tượng người dùng phản hồi với các toán tử như +. Chúng ta sẽ tìm hiểu chi tiết hơn về điều này trong Chương 16, nhưng ở đây mục tiêu của chúng ta là minh họa thêm về việc sử dụng các phương thức đặc biệt thông qua một ví dụ đơn giản khác.

Chúng ta sẽ triển khai một lớp để biểu diễn các vectơ hai chiều - tức là các vectơ Euclide giống như các vectơ được sử dụng trong toán học và vật lý.

Chúng ta sẽ bắt đầu thiết kế API cho lớp đó bằng cách viết một phiên giao diện điều khiển mô phỏng mà chúng ta có thể sử dụng sau này như một doctest. Đoạn mã sau kiểm tra phép cộng vectơ được mô tả trong Hình 1-1:

>>> v1 = Vector(2, 4)
>>> v2 = Vector(2, 1)
>>> v1 + v2
Vector(4, 5)

Lưu ý cách toán tử + tạo ra một Vector mới, được hiển thị ở định dạng thân thiện trên giao diện điều khiển.

Hàm abs tích hợp sẵn trả về giá trị tuyệt đối của số nguyên và số thực, và độ lớn của số phức, vì vậy để nhất quán, API của chúng ta cũng sử dụng abs để tính độ lớn của một vectơ:

>>> v = Vector(3, 4)
>>> abs(v)
5.0

Chúng ta cũng có thể triển khai toán tử * để thực hiện phép nhân vô hướng (tức là nhân một vectơ với một số để tạo ra một vectơ mới có cùng hướng và độ lớn được nhân lên):

>>> v * 3
Vector(9, 12)
>>> abs(v * 3)
15.0

Giải thích:

Đoạn văn này đang nói về việc sử dụng các phương thức đặc biệt trong Python để cho phép các đối tượng do người dùng định nghĩa (trong trường hợp này là lớp Vector) hoạt động giống như các kiểu số tích hợp sẵn (như int, float).

Cụ thể, đoạn văn mô tả cách triển khai các phương thức đặc biệt để:

Cho phép sử dụng toán tử + để cộng hai vectơ.
Cho phép sử dụng hàm abs() để tính độ lớn của một vectơ.
Cho phép sử dụng toán tử * để nhân một vectơ với một số (phép nhân vô hướng).

Việc sử dụng các phương thức đặc biệt này giúp cho việc làm việc với các đối tượng do người dùng định nghĩa trở nên trực quan và dễ dàng hơn, giống như khi làm việc với các kiểu dữ liệu tích hợp sẵn.

import math 

class Vector:
    def __init__(self, x, y):
        self.x = x
        self.y = y 
    
    def __repr__(self):
        return f'Vector({self.x!r}, {self.y!r})' # !r để  biến self.x và self.y từ số thành string
    
    def __abs__(self):
        return math.hypot(self.x, self.y)
    
    def __bool__(self):
        return bool(abs(self))
    
    def __add__(self, other):
        x = self.x + other.x
        y = self.y + other.x 
        return Vector(x, y)
    
    def __mul__(self, scalar):
        return Vector(self.x * scalar, self.y * scalar)

2.2. String Representation

Phương thức đặc biệt __repr__ được gọi bởi hàm repr() tích hợp sẵn để lấy biểu diễn chuỗi của một đối tượng để kiểm tra. Nếu không có __repr__ tùy chỉnh, console của Python sẽ hiển thị một instance của Vector là <Vector object at 0x10e100070>.

Console tương tác và trình gỡ lỗi gọi repr() trên kết quả của các biểu thức được đánh giá, cũng như trình giữ chỗ %r trong định dạng cổ điển với toán tử %, và trường chuyển đổi !r trong cú pháp chuỗi định dạng mới được sử dụng trong f-string và phương thức str.format.

Lưu ý rằng f-string trong __repr__ của chúng ta sử dụng !r để lấy biểu diễn chuẩn của các thuộc tính sẽ được hiển thị. Đây là một cách thực hành tốt, vì nó cho thấy sự khác biệt quan trọng giữa Vector(1, 2) và Vector('1', '2') - cái sau sẽ không hoạt động trong ngữ cảnh của ví dụ này, vì các đối số của hàm tạo phải là số, không phải chuỗi.

Chuỗi được trả về bởi __repr__ phải rõ ràng và nếu có thể, khớp với mã nguồn cần thiết để tạo lại đối tượng được biểu diễn. Đó là lý do tại sao biểu diễn Vector của chúng ta trông giống như gọi hàm tạo của lớp (ví dụ: Vector(3, 4)).

Ngược lại, __str__ được gọi bởi hàm str() tích hợp sẵn và được hàm print sử dụng ngầm định. Nó nên trả về một chuỗi phù hợp để hiển thị cho người dùng cuối.

2.3. Boolean Value of a Custom Type

Mặc dù Python có kiểu dữ liệu bool, nó chấp nhận bất kỳ đối tượng nào trong ngữ cảnh Boolean, chẳng hạn như biểu thức điều khiển câu lệnh if hoặc while, hoặc toán hạng của and, or và not. Để xác định xem một giá trị x là “truthy” (đúng) hay “falsy” (sai), Python áp dụng hàm bool(x), trả về True hoặc False.

Theo mặc định, các instance của các lớp do người dùng định nghĩa được coi là “truthy”, trừ khi phương thức __bool__ hoặc __len__ được triển khai. Về cơ bản, bool(x) gọi x.__bool__() và sử dụng kết quả. Nếu __bool__ không được triển khai, Python cố gắng gọi x.__len__(), và nếu nó trả về 0, bool trả về False. Nếu không, bool trả về True.

Ví dụ, triển khai __bool__ đơn giản là trả về False nếu độ lớn của một vector bằng 0, True trong trường hợp khác. Ta chuyển đổi độ lớn thành Boolean bằng cách sử dụng bool(abs(self)) vì __bool__ được mong đợi trả về một Boolean. Ngoài phương thức __bool__, hiếm khi cần gọi bool() một cách rõ ràng, vì bất kỳ đối tượng nào cũng có thể được sử dụng trong ngữ cảnh Boolean.

Lưu ý cách phương thức đặc biệt __bool__ cho phép các đối tượng của bạn tuân theo các quy tắc kiểm tra giá trị Boolean được định nghĩa trong chương “Built-in Types” của tài liệu The Python Standard Library.

2.4. Collection API

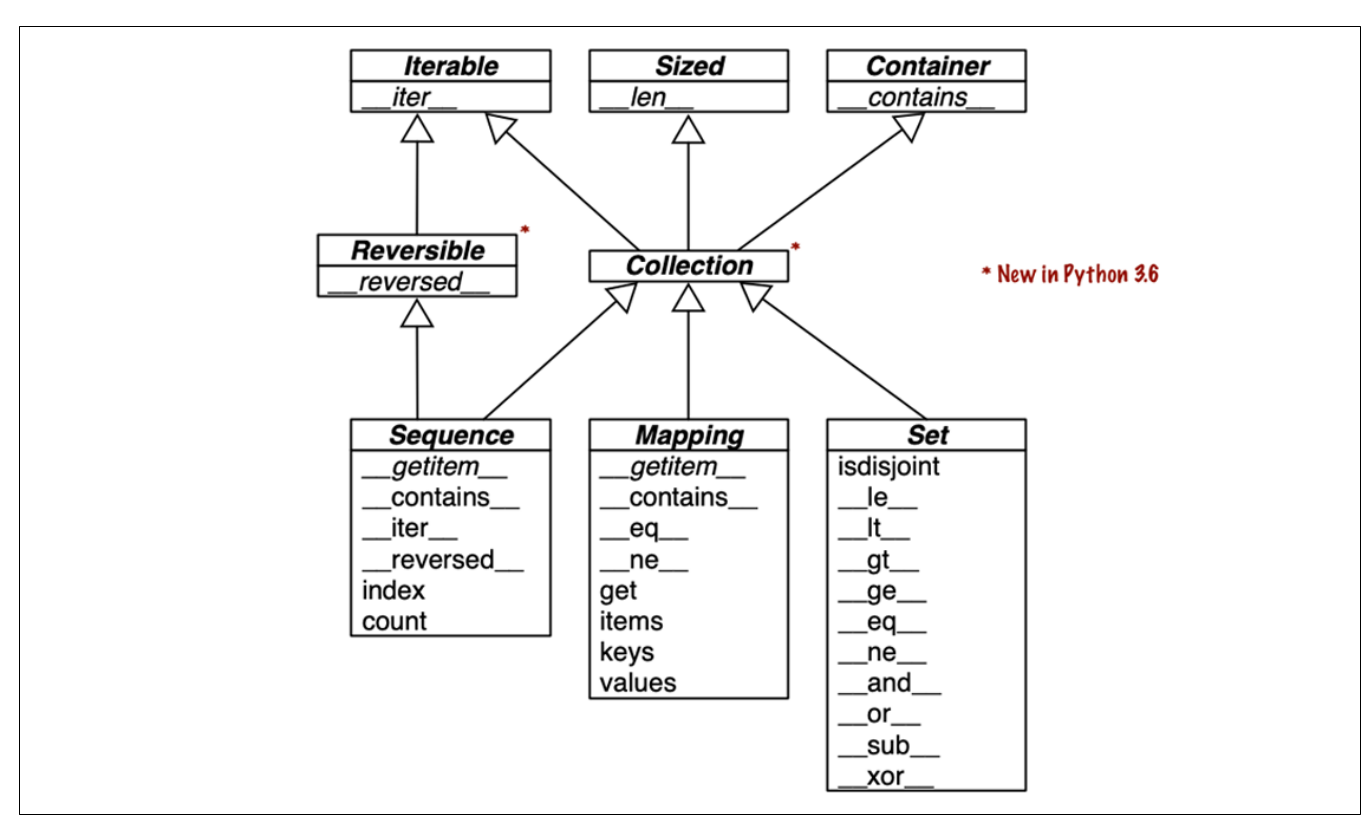
Collection API ghi lại các interfaces của các kiểu tập hợp thiết yếu trong ngôn ngữ. Tất cả các lớp trong sơ đồ là các ABC - lớp cơ sở trừu tượng. Các ABC và module collections.abc được đề cập trong Chương 13. Mục tiêu của phần ngắn gọn này là cung cấp cái nhìn tổng quan về các giao diện tập hợp quan trọng nhất của Python, cho thấy cách chúng được xây dựng từ các phương thức đặc biệt.

Mỗi ABC hàng đầu có một phương thức đặc biệt duy nhất. ABC Collection (mới trong Python 3.6) thống nhất ba giao diện thiết yếu mà mọi tập hợp nên triển khai:

Iterable: để hỗ trợ vòng lặp for, giải nén và các dạng lặp khác.
Sized: để hỗ trợ hàm dựng sẵn len.
Container: để hỗ trợ toán tử in.

Python không yêu cầu các lớp cụ thể phải thực sự kế thừa từ bất kỳ ABC nào trong số này. Bất kỳ lớp nào triển khai __len__ đều thỏa mãn giao diện Sized.

Ba đặc tả rất quan trọng của Collection là:

Sequence: chính thức hóa giao diện của các kiểu dựng sẵn như list và str.
Mapping: được triển khai bởi dict, collections.defaultdict, v.v.
Set: giao diện của các kiểu dựng sẵn set và frozenset.

Chỉ có Sequence là Reversible (khả nghịch), vì các chuỗi hỗ trợ thứ tự tùy ý của nội dung của chúng, trong khi các ánh xạ và tập hợp thì không.

Tất cả các phương thức đặc biệt trong ABC Set đều triển khai các toán tử trung tố. Ví dụ: a & b tính toán giao điểm của các tập hợp a và b và được triển khai trong phương thức đặc biệt __and__.

3. Overview of Special Methods

Chương “Data model” trong The Python Language Reference liệt kê hơn 80 tên phương thức đặc biệt. Hơn một nửa trong số chúng triển khai các toán tử số học, bit và so sánh. Để có cái nhìn tổng quan về những gì có sẵn, hãy xem các bảng sau.

Bảng 1-1 hiển thị các tên phương thức đặc biệt, ngoại trừ những phương thức được sử dụng để triển khai các toán tử trung tố hoặc các hàm toán học cốt lõi như abs. Hầu hết các phương thức này sẽ được đề cập trong suốt cuốn sách, bao gồm các bổ sung gần đây nhất: các phương thức đặc biệt không đồng bộ như anext (được thêm vào trong Python 3.5) và hook tùy chỉnh lớp, init_subclass (từ Python 3.6).

Các toán tử trung tố và số học được hỗ trợ bởi các phương thức đặc biệt được liệt kê trong Bảng 1-2. Ở đây, các tên gần đây nhất là __matmul__, __rmatmul__ và __imatmul__, được thêm vào trong Python 3.5 để hỗ trợ việc sử dụng @ làm toán tử trung tố cho phép nhân ma trận, như chúng ta sẽ thấy trong Chương 16.

Toán tử trung tố (infix operators): Như đã giải thích trước đó, là các toán tử được đặt giữa hai toán hạng (ví dụ: a + b).
Toán tử số học (numerical operators): Là các toán tử thực hiện các phép toán số học như cộng (+), trừ (-), nhân (*), chia (/), v.v.
__matmul__, __rmatmul__, __imatmul__: Đây là các phương thức đặc biệt được sử dụng để định nghĩa hành vi của toán tử @ khi thực hiện phép nhân ma trận.
- __matmul__: Xử lý phép nhân ma trận thông thường (ví dụ: a @ b).
- __rmatmul__: Xử lý phép nhân ma trận khi toán hạng trái không hỗ trợ __matmul__ (ví dụ: b @ a khi b không có __matmul__).
- __imatmul__: Xử lý phép nhân ma trận với gán (ví dụ: a @= b, tương đương với a = a @ b).

4. Why len Is Not a Method

Tại sao len không phải là một phương thức?

Tôi đã hỏi câu hỏi này cho nhà phát triển cốt lõi Raymond Hettinger vào năm 2013, và chìa khóa cho câu trả lời của ông ấy là một câu trích dẫn từ “The Zen of Python”: “Tính thực tế đánh bại sự thuần túy.” Trong “Cách sử dụng các phương thức đặc biệt” ở trang 8, tôi đã mô tả cách len(x) chạy rất nhanh khi x là một thể hiện của một kiểu dữ liệu dựng sẵn. Không có phương thức nào được gọi cho các đối tượng dựng sẵn của CPython: độ dài chỉ đơn giản được đọc từ một trường trong cấu trúc C. Việc lấy số lượng phần tử trong một tập hợp là một thao tác phổ biến và phải hoạt động hiệu quả cho các kiểu dữ liệu cơ bản và đa dạng như str, list, memoryview, v.v.

Nói cách khác, len không được gọi như một phương thức vì nó được xử lý đặc biệt như một phần của Mô hình dữ liệu Python, giống như abs. Nhưng nhờ phương thức đặc biệt __len__, bạn cũng có thể làm cho len hoạt động với các đối tượng tùy chỉnh của riêng mình. Đây là một sự thỏa hiệp hợp lý giữa nhu cầu về các đối tượng dựng sẵn hiệu quả và tính nhất quán của ngôn ngữ.

Cũng từ “The Zen of Python”: “Các trường hợp đặc biệt không đủ đặc biệt để phá vỡ các quy tắc.”

Giải thích thêm :

len: Là một hàm dựng sẵn trong Python được sử dụng để lấy độ dài của một đối tượng (ví dụ: chuỗi, danh sách, tuple).
Tính thực tế đánh bại sự thuần túy (practicality beats purity): Trong trường hợp này, việc tối ưu hóa hiệu suất của len cho các kiểu dữ liệu dựng sẵn được ưu tiên hơn việc tuân thủ nghiêm ngặt nguyên tắc hướng đối tượng (trong đó mọi thứ đều là đối tượng và mọi thao tác đều được thực hiện thông qua phương thức).
CPython: Là triển khai tham chiếu của ngôn ngữ Python, được viết bằng C.
Cấu trúc C (C struct): Là một kiểu dữ liệu trong C cho phép nhóm các biến có kiểu dữ liệu khác nhau thành một đơn vị.
Mô hình dữ liệu Python (Python Data Model): Là tập hợp các quy tắc và quy ước xác định cách các đối tượng hoạt động trong Python, bao gồm các phương thức đặc biệt.
__len__: Là một phương thức đặc biệt cho phép bạn định nghĩa cách hàm len hoạt động với các đối tượng của lớp bạn tạo ra.
Các trường hợp đặc biệt không đủ đặc biệt để phá vỡ các quy tắc (Special cases aren’t special enough to break the rules): Mặc dù len được xử lý đặc biệt, nhưng nó vẫn tuân theo quy tắc chung của Mô hình dữ liệu Python bằng cách cho phép bạn tùy chỉnh hành vi của nó thông qua phương thức đặc biệt __len__.

Tóm lại, lý do tại sao len không phải là một phương thức trong Python. Đó là vì lý do hiệu suất và len được xử lý đặc biệt trong Mô hình dữ liệu Python. Tuy nhiên, Python vẫn duy trì tính nhất quán bằng cách cho phép lập trình viên tùy chỉnh hành vi của len thông qua phương thức đặc biệt __len__.